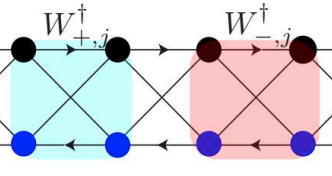
Interaction induced itinerancy and bulk-edge correspondence
Bosonic particle pair of the Creutz ladder become itinerant due to particle-particle interaction although its one particle spectrum is completely flat implying localized in real space. Then modulatio...
Read More
名古屋大学 特別講義 令和2年12月
名古屋大学 特別講義 令和2年12月14日-16日 (河野浩先生ご紹介) 講義 "Physics of bulk-edge correspondence:From quantum Hall effects to recent topics" 談話会 "Flat bands and topological phases" 予定 01-対称性の破れからトポロシ...
Read More
BEC seminar 2020年12月18日(金)14:00-15:00 : 水田郁 さん(京都大学)
BEC seminar, 14:00-15:00 Dec.18 (2020)にて水田郁 さん(京都大学)に以下のタイトルで最近のご研究についてお話し頂きます。 “Liouvillianity breaking in interacting Floquet-Lindblad systems under high-frequency drive”。 よろしくお願いいたします。
Read More
科学新聞に掲載されました:第三種ディラックコーンを微調整なしにつくる!
第三種ディラックコーンの作り方についての記事が令和2年11月13日の科学新聞 : に掲載されました。関係する仕事はこちら。
Read More
Thouless pump and SPT’s phase boundary
Thouless' (adiabatic) pump in one-dimension is a typical topological phenomena characterized by the Chern number that correspondes to the quantized motion of the center of mass (COM). Although the...
Read More
Comming events before 2020
--- Coming event ------------------------------ --- 2020 ------------------------------ 名古屋大学 特別講義 , Dec.14-16 (2020): hosted by Prof. Hiroshi Kohno 日本物理学会 2020年秋季大会 online , Sep.8-11 (2020) 筑波大学数学域「数...
Read More
Editors’ choice and News & Comm. of JPSJ: Type III Dirac cones…
The Dirac cone is a typical singular energy dispersion in two dimensions that is a source of various non-trivial topological effects. When realized in real/synthetic materials, it is generically tilte...
Read More
Square-root higher order topological insulator (SR-HOTI)
Motivated by a historical example, the Dirac Hamiltonian as a square-root of the Klein-Gordon Hamiltonian, its lattice analogue has been discussed recently. Zero energy states are shared by the parent...
Read More
量子力学3(2020)(筑波大学)
2020年度量子力学3(遠隔講義)講義(初貝安弘),演習(吉田恒也),TA(若尾洋正,南島元) 量子力学における対称性の議論の基礎を学び,回転操作に関連する角運動量について詳しく議論する。その後,量子力学と群の関係の基礎についても学ぶ。 履修登録者は 筑波大学学内microsoft streamでの動画は で「量子力学」を検索。 注意iOSではスクロールしません。PCにてご覧ください。 講義ノー...
Read More
外部資金(2020)
科学研究費補助金 科研費データベース 初貝安弘 プロジェクト 基盤研究S : トポロジカル相でのバルク・エッジ対応の多様性と普遍性:固体物理を越えて分野横断へ 研究課題番号:17H06138 205,140千円 (直接経費 : 157,800千円、間接経費 : 47,340千円) May 31, 2017 - March 31, 2022 2017年度 : 45,370千円 (直接経費 : 34,...
Read More
公募のお知らせ : 助教1名(2019)
物性理論(トポロジカル相の理論的または数値的研究, 量子系または古典系のバルクエッジ対応等) 助教1名。 。 応募締め切り 2019年8月31日(土)。電子メールにて応募。関係者まで周知頂けますと幸いです
Read More
公募のお知らせ : 助教1名(2019)
物性理論(トポロジカル相の理論的または数値的研究, 量子系または古典系のバルクエッジ対応等) 助教1名。 。 応募締め切り 2019年8月31日(土)。電子メールにて応募。関係者まで周知頂けますと幸いです
Read More
九州大学集中講義 平成30年(2018年)7月
「トポロジカル相の発見とその展開」九州大学大学院理学研究科 集中講義 (野村清英 先生 ご紹介)平成30年7月17日-19日 概要量子ホール効果の発見にはじまり,Haldane相,グラフェン,トポロジカル絶縁体,ワイル半金属,そして量子系以外のフォトニック結晶や古典力学系のトポロジカル相にも多彩に展開したトポロジカル相に関してその基礎から講義する。特にベリー接続,対称性の保護とバルク・エッジ対応に...
Read More
公募のお知らせ:助教2名(トポロジカル相の理論)(2017)
公募PDFファイル 2017年7月1日 関係機関各位 筑波大学大学院数理物質科学研究科 物理学専攻長 守友 浩 前略 本専攻では,下記の要領で専任教員を公募することになりました。つきましては,貴機関関係各位にご周知いただくとともに,適任者のご推薦または応募についてご配慮いただきますようお願い申し上げます.草々 記 公募人員: 助教2名(助教A,助教B) 所属組織: 数理...
Read More
千葉大学集中講義(2015)
千葉大学大学院理学研究科 物理集中講義 (中山隆史 先生 ご紹介) 平成27年7月8日-9日 概要 近年、トポロジカル絶縁体およびグラフェンが実験的に合成されたことを契機に関連物質が多くの興味を集めているが、これらは全て系の境界に特徴的な局在状態であるエッジ状態が存在しその起源は系に境界のないバルクの電子状態にあり、逆にまたバルクの電子状態はエッジ状態により特徴づけられると考えられる「バルク・エッ...
Read More
統計力学2 (2013)
統計力学2 (2013) : 筑波大学理工学群物理学類 ・学部3年 I. 量子統計力学 (新版は後ろに) 密度行列 量子理想気体 II. 協力現象と相転移 平均場近似 ランダウ理論 III. 散逸のある系 ブラウン運動 ランジュバン方程式 因果律とクラマース・クローニッヒの関係 P. 演習問題 第1回演習問題 第2回演習問題 第3回演習問題 第4回演習問題 第5回演習問題 第6回演習問題 第7回...
Read More
茗渓学園コアSSH(対称性とその自発的破れ)
2013年9月1日に茗渓学園コアSSH APサイエンス学習会で話をしました。高校生向け。 講演ファイル
Read More
トポロジカル相以前のトポロジカル相
昔の科研費 科研費 1992年度:電子系スピン系におけるトポロジカル効果 科研費 1994年度:物性論におけるトポロジーと幾何学的位相 私の講演ファイルのいくつか MIT, Boston (2003) APS/JPS March Meeting (2004) JPS Fall meeting, JAPAN (2004) APS/JPS March meeting (2005) JPS F...
Read More
力学A (2012)
力学A (2012):物理学類1年生対象(大学初年度) 物理学における基礎科目として、質点の運動を丁寧に学ぶ。その際、概念的には普遍性の重要性、座標変換の意義、保存則等について学び、技術的には物理学において必要とされる基礎的な数学(微分方程式、線形代数、ベクトル解析)の一部★を厳密性は犠牲にしても理解できて使える算術の方法として自己完結的に講義する。また適宜レポート問題を主とする演習を行う。 一...
Read More