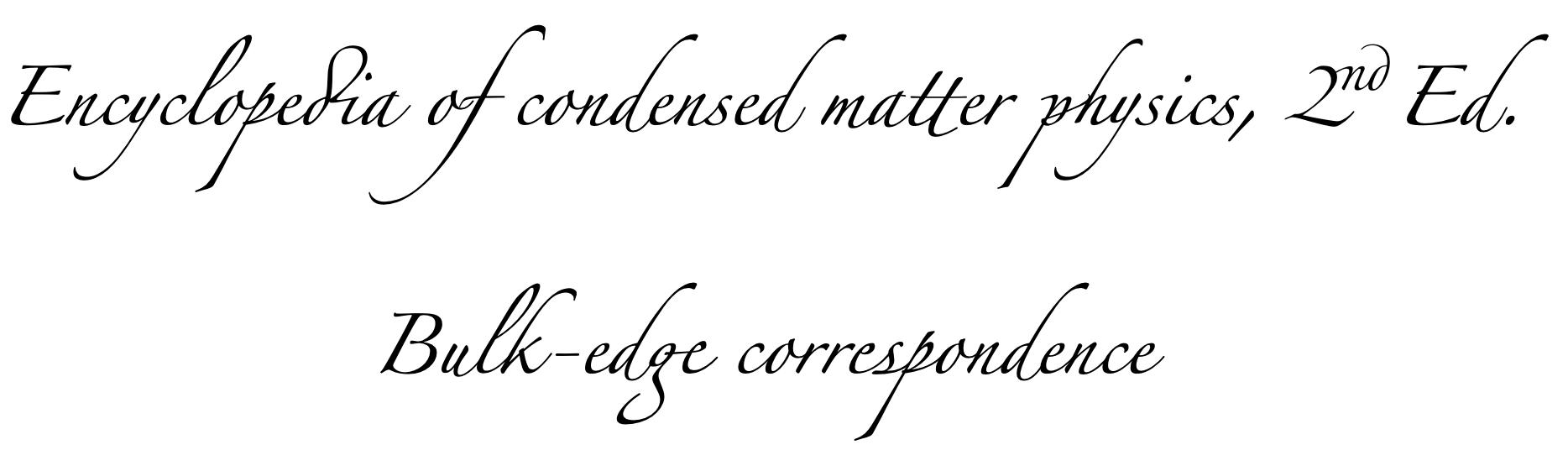Nonlinearity and topology in 1D
Hatsugai – 2026.1.5
Nonlinearity is surely an old and hard problem, as history shows. Topological physics may provide a new viewpoint for it. The paper "Topological-to-topological transition induced by on-site nonli...
Read More
One more thing, a set of plateaux transitions of multi-leg spin ladder
Hatsugai – 2025.12.5
A set of new plateaux transitions of multi-leg spin pump has been found and characterized topologically. The model is constructed by introducing staircase clusters. Topological numbers of the bulk and...
Read More
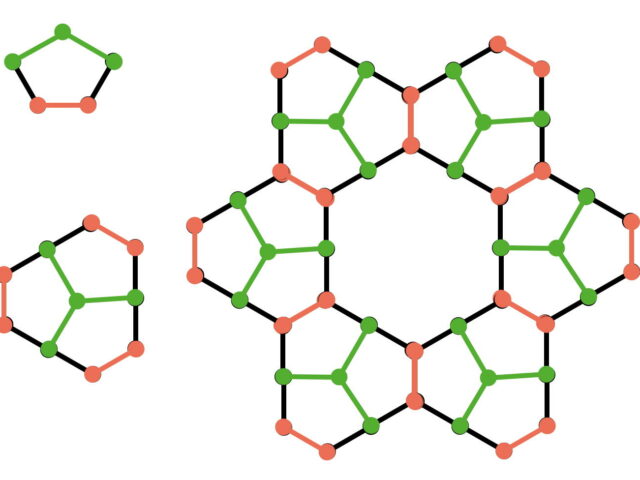
Flatband of pentagons
Hatsugai – 2025.7.27
Flatband is everywhere. A tight-binding Hamiltonian of a pentagon network of atoms is proposed that possesses a flat band (although it needs fine-tuning) in our recent paper, "Evolution of flat b...
Read More
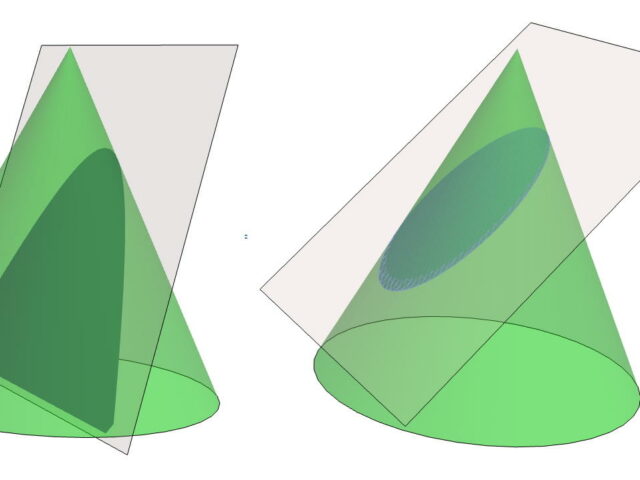
Conic section & generalized eigenvalue problem
Hatsugai – 2025.6.19
A generalized eigen value problem, that is described by two hermitian Hamiltonian/overlap matrices, intrisically posesses a conic structure that may induce complex eigen values. The story is geometica...
Read More
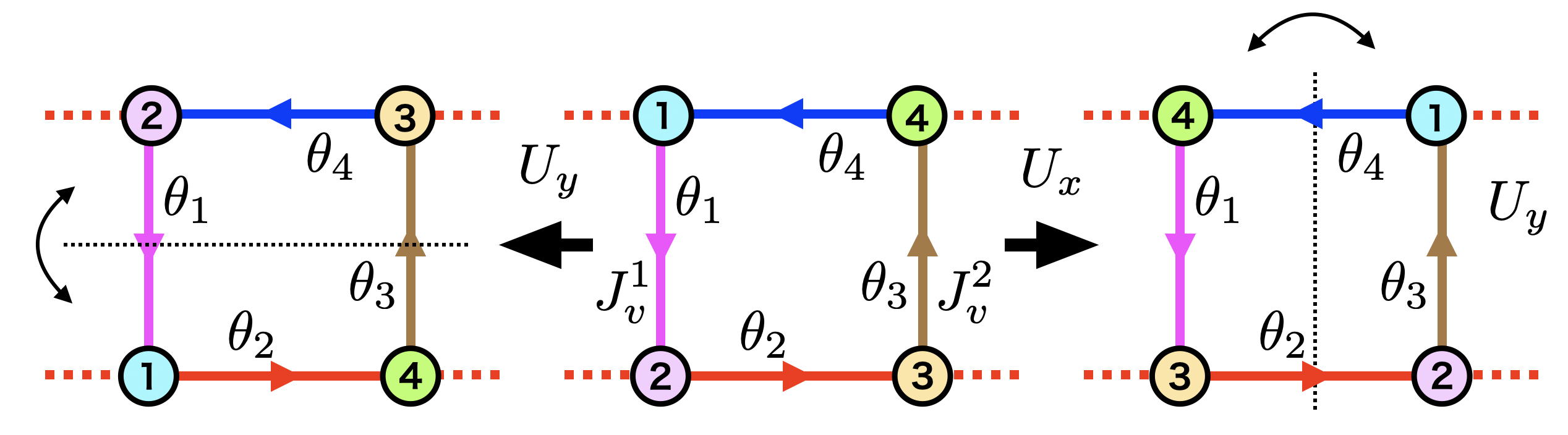
Non trivial domain wall pump with SSB
Hatsugai – 2025.5.10
The gauge field is associated with the connection, which implies that it lives on the link as for the gauge transformation acting on the sites. In contrast, the domain wall we discussed in the recent ...
Read More
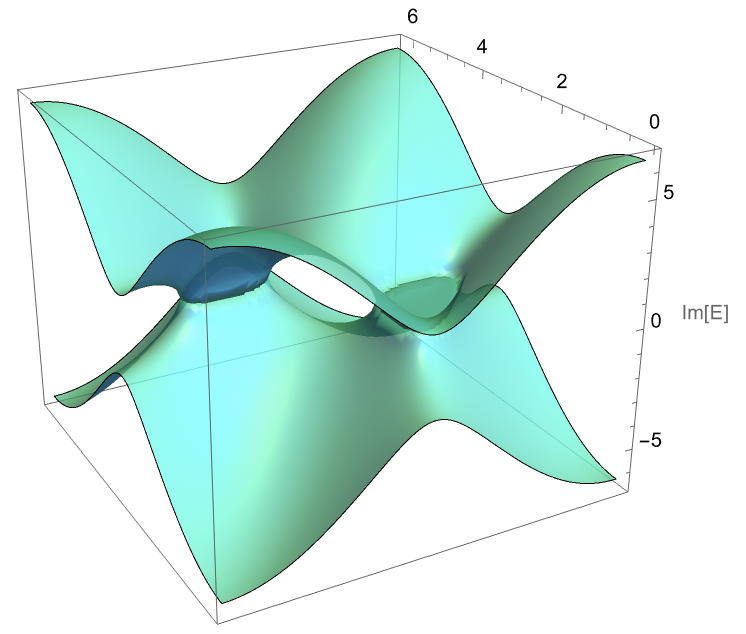
EP and non-Hermitian physics in nonlinearity of eigenvalues
Hatsugai – 2025.5.9
When one considers a frequency dependent system, it can be reduced to an eigen value problem which depends on the eigen value itself, that is, a non-linear eigen value problem. It hosts an exceptional...
Read More
ZN Berry phases of Pyrochlore magnet
Hatsugai – 2025.3.13
Various symmetry-protected topological phases of quantum spins on a breathing Pyrochlore are discussed by the Quantum Monte Carlo method. ZN Quantized Berry phases( N=2,3,4,6) are directly evaluated a...
Read More
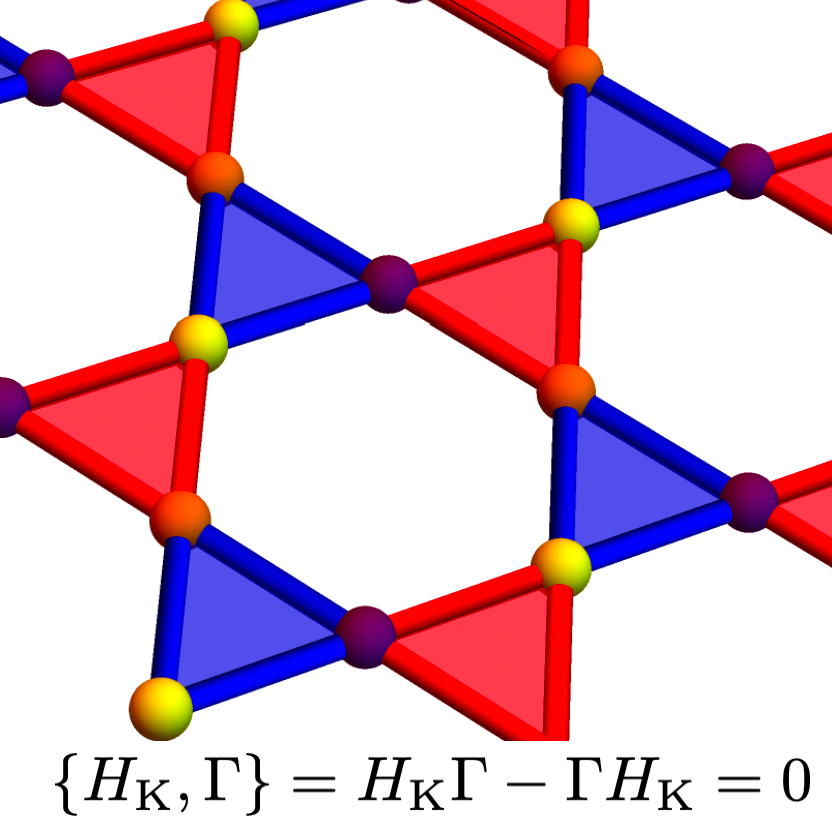
Kagome lattice is chiral symmetric
Hatsugai – 2025.3.3
Chiral symmetry in condensed matter physics implies the sublattice symmetry (as far as the one-particle hopping Hamiltonian is concerned). Then the usual belief is that the nearest neighbor hopping Ha...
Read More
Exceptional points of metamaterials induced by nonlinearity of eigenvalues
Hatsugai – 2025.2.14
Exceptional points (Eps) are common in metamaterials if one generically considers nonlinearity of eigenvalues that is also quite common in reality. We have considered these kinds of EP topologically a...
Read More
Z3 Berry phases for quantum spins
Hatsugai – 2024.5.22
Z3 Berry phases for XXZ quantum spins on Kagome lattice are calculated by the quantum Monte Carlo method under a condition with fixed magnetization. The phase diagram of the model is discussed by usin...
Read More
Non-uniform flux and particle blocking
Hatsugai – 2024.5.4
Spatial variation of physical parameters may induce rich phenomena, which can only be realized in artificial structures by meta-materials and cold atoms. Non-uniform flux associated with particle bloc...
Read More
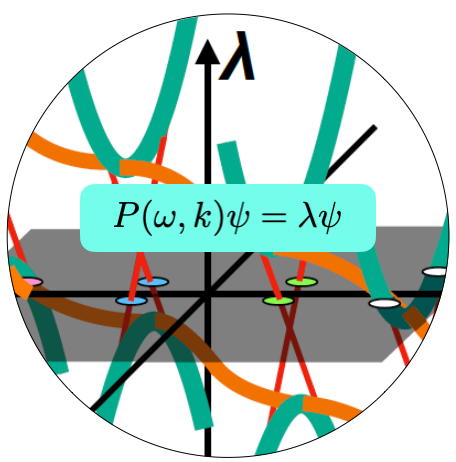
Bulk-edge correspondence for energy dependent systems/nonlinear eigen value problems
Hatsugai – 2024.3.19
The recent development of a topological description of matter, especially for classical systems, is based on the formal analogy to quantum mechanics. The differential equation governing the classical ...
Read More
Bulk-edge correspondence (Encyclopedia of condensed matter physics, 2nd Ed.)
Hatsugai – 2023.12.14
I wrote a chapter on the bulk-edge correspondence in Encyclopedia of condensed matter physics, 2nd Ed.,Volume 1, 2024, Pages 659-669, Its abstract is free.
Read More
Nontrivial Topology of Nontopological Nonlinear Waves
Hatsugai – 2023.8.22
I have written an article for JPSJ News & Comments. Have a look at "Nontrivial Topology of Nontopological Nonlinear Waves." See also old ones. "Y. Hatsugai, News Comments 20, 10 (20...
Read More
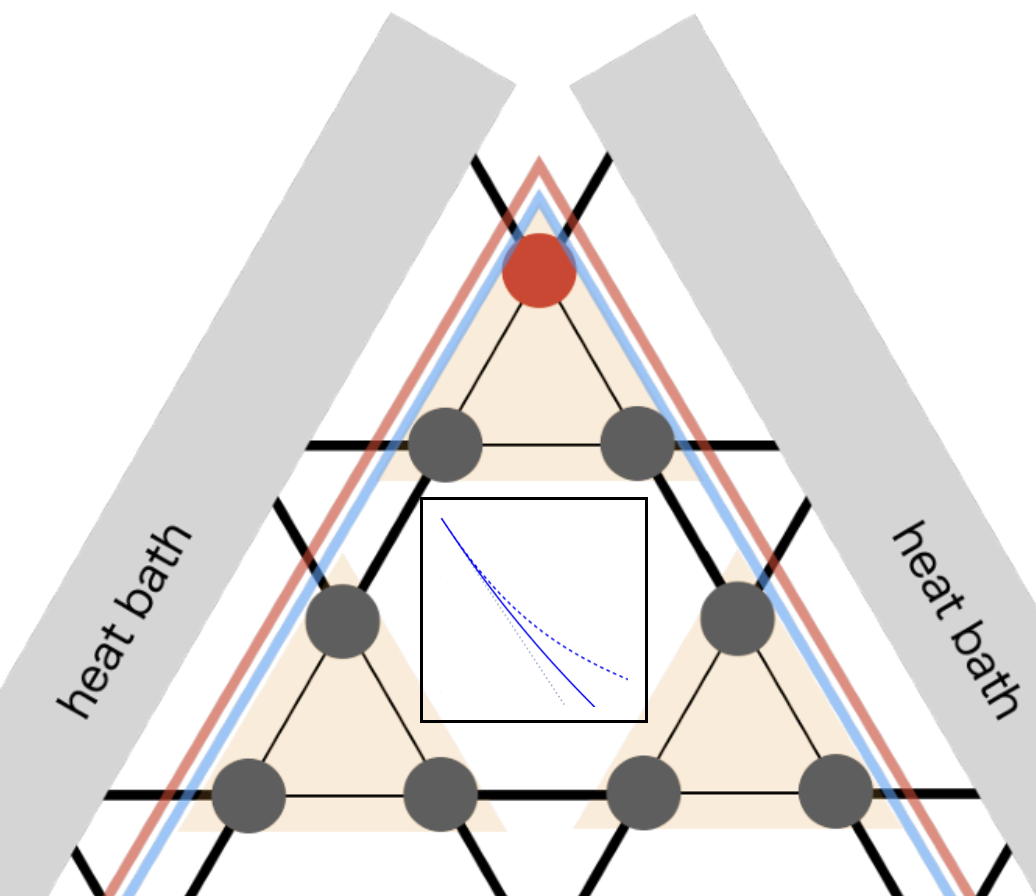
Heat carrying corner states of breathing Kagome
Hatsugai – 2023.7.20
Heat conduction of the breathing Kagome lattice is discussed in relation to the anomalous heat-carrying corner states due to higher-order topology. Especially the use of the effective Hamiltonian for ...
Read More
Z2× Z2 symmetry and Z4 quantization in bosonic ladders
Hatsugai – 2023.7.14
A two-leg ladder is a nice place to discuss Z2× Z2 symmetry with sufficient numerical accuracy. Using a Z4 Berry phases, several phases of bosonic ladders are discussed in relation to the bulk-edge co...
Read More
Negative index photonic crystal induces non hermitian physics
Hatsugai – 2023.6.15
An electromagnetic field in a photonic crystal is described by a hermitian eigenvalue problem with an overlap matrix which may not be positive definite if the system is composed of negative index medi...
Read More
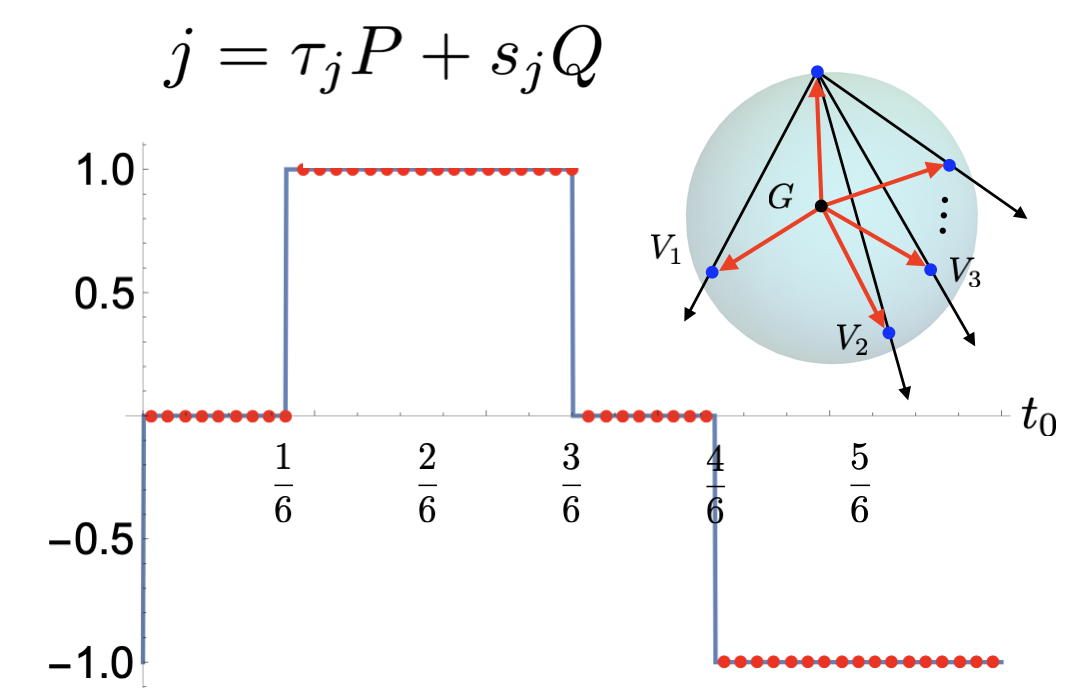
Diophantine equation of SU(Q) topological pump
Hatsugai – 2023.6.2
A topological pump of SU(Q) interacting fermions is proposed based on Affleck's SU(Q) quantum chains associated with a symmetric breaking term characterized by a parameter P/Q with co-prime intege...
Read More
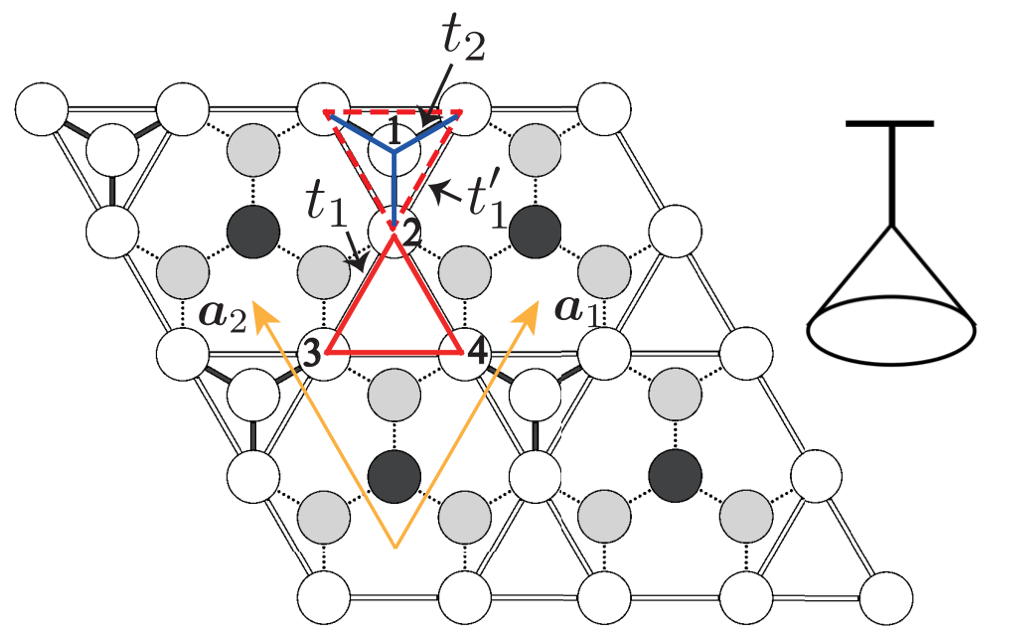
Graphene, silicene and martini
Hatsugai – 2023.2.22
Chemisorption on graphene and silicene may realize Martini type π-electron network. It implies specific band dispersion. We propose potential materialization by using the molecular orbital constr...
Read More
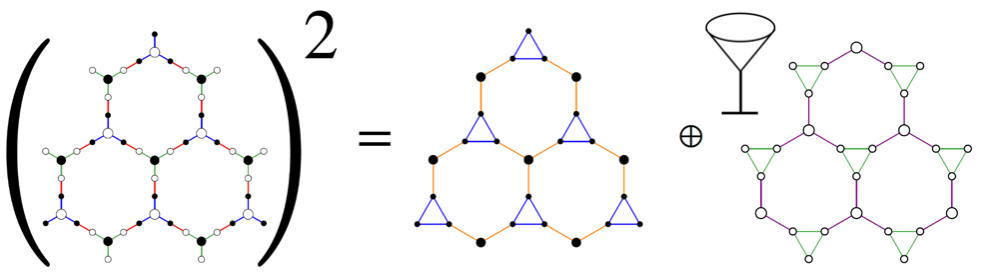
Array of Martini glasses with topology
Hatsugai – 2023.2.22
Taking a square root is not trivial. The Dirac equation is invented by the square root of the Kleind-Gordon equation. Then the lattice analog of the operation implies non-trivial topology and edge/cor...
Read More