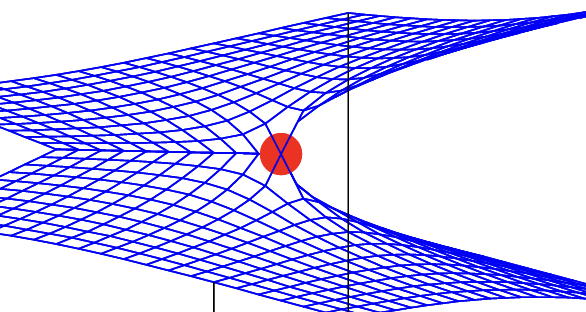
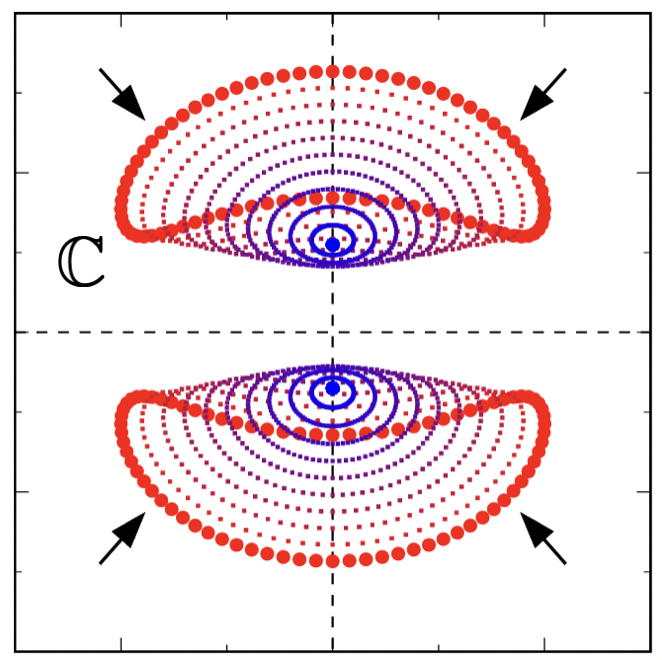
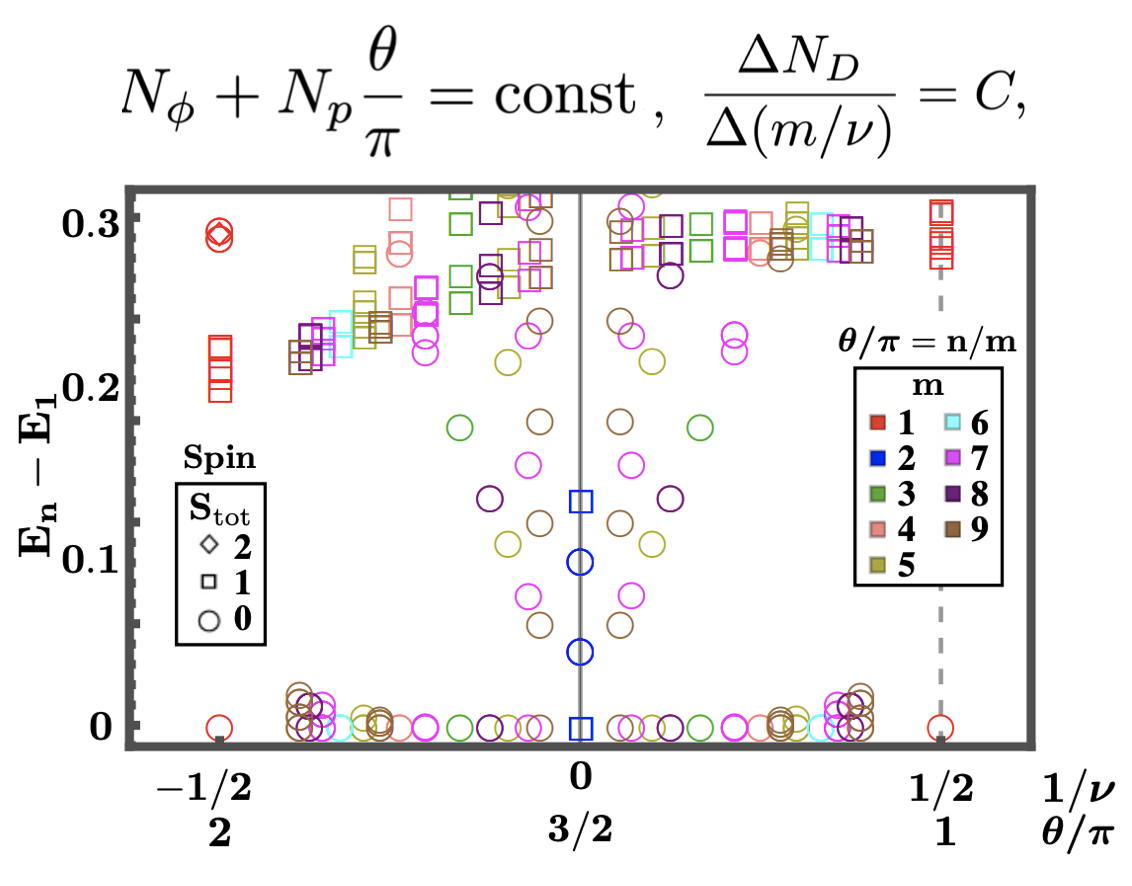
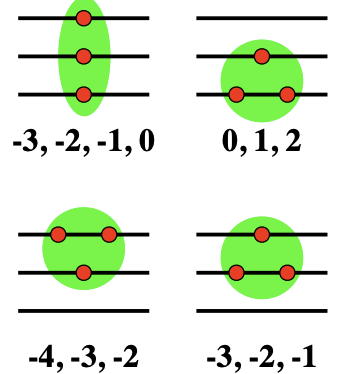
Topological strucure can be fragile against interactions
Topological protection of singularities for the non-Hermitian problem is one of the recent focuses in condensed matter physics. Exceptional points and rings with symmetry constraints are typical examp...
Read More
Seminar by Tonomari Mizoguchi
Coming Wed. afternoon, 13:00, Dec.14, Tomonari Mizoguchi (Univ. Tsukuba) will be telling us about his work in collaboration with N. Okuma (Kyoto Univ.). The seminar is in a hybrid format. Please conta...
Read More
Reduction of non-Hermitian 1D topology with interaction
Topological protection for topological systems may change by the inclusion of particle-particle interaction, which is known as "reduction phenomena." Here we have pointed out its possibiliti...
Read More
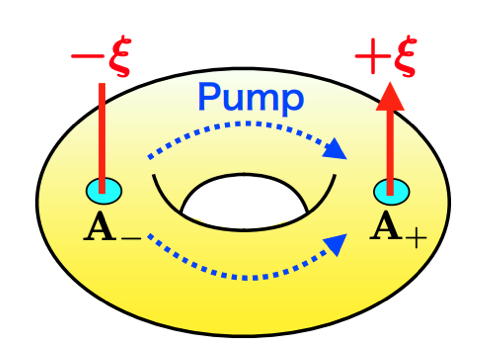
Bulk-edge correspondence in electric circuits of topological pump
One of the recent wisdom for topological phases is the use of a classical system as a quantum simulator. The Hofstadter butterfly associated with topological phase transitions is realized in electric ...
Read More
Localization 2022
Localisation 2022 T. Mizoguchi and Y. Hatsugai, "Gap opening and emergent critical states in a random-phase molecular-orbital model", Localisation 2022, Aug.25-30 (2022) T. Kuroda, T. Mizogu...
Read More
Adiabatic connection with spin
Adiabatic connection of the gapped many-body states is a conceptual background of the topological phases. Historical and more than successful examples are given by various fractional quantum Hall stat...
Read More
BEC seminar by Koji Kudo, Aug.10, 2022
On Aug.10 (Wed) 2022 at 11:am Japan time, Koji Kudo at Penn State will be telling us about his recent study by a title : "Exactly solvable model for non-Abelian quasiparticle states." Join u...
Read More
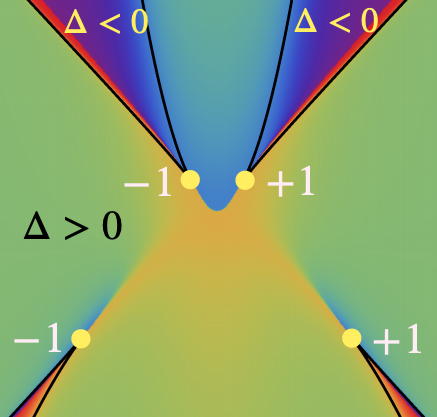
“b 2– 4 ac” formula with rotation symmetry
The discriminant is a generalization of the "b 2- 4 ac" formula that everybody knows, which tells us the degeneracy of the (secular) equation. Then it is natural the discriminant is useful f...
Read More
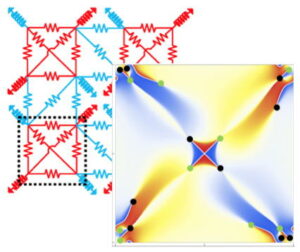
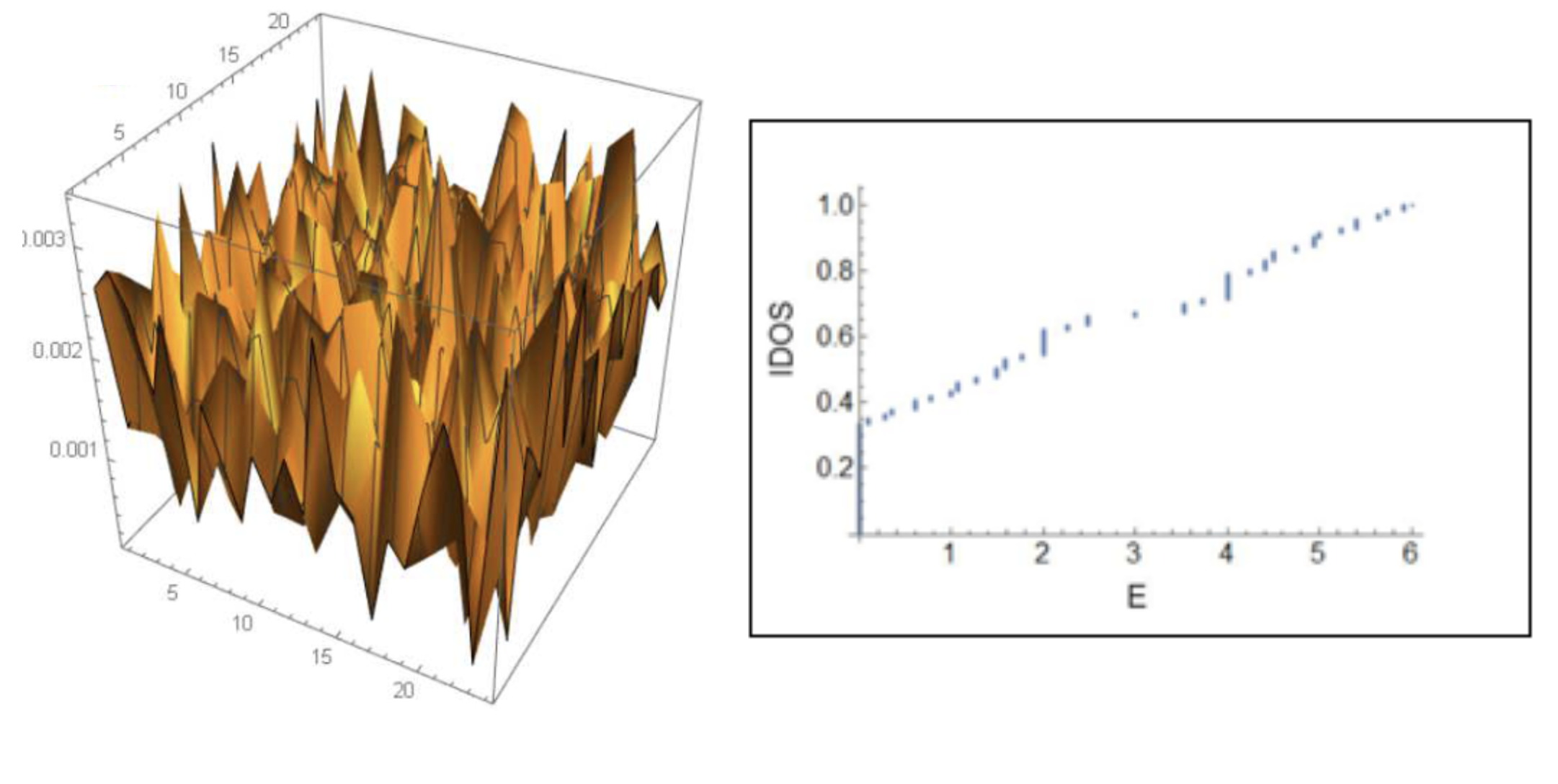
Random flatbands are special
Recent wisdom for the construction of flat bands is applicable even with randomness. Characterization of special features of the random flat bands has been successfully done by using machine learning....
Read More
APS March meeting 2022
APS March meeting, March 14-18 2022, Chicago USA Fractional charge pumping of anyons and the adiabatic heuristic principle Wed, March 16, 8:06 a.m.—8:18 a.m. Presenter: Koji Kudo(University of Tsukuba...
Read More
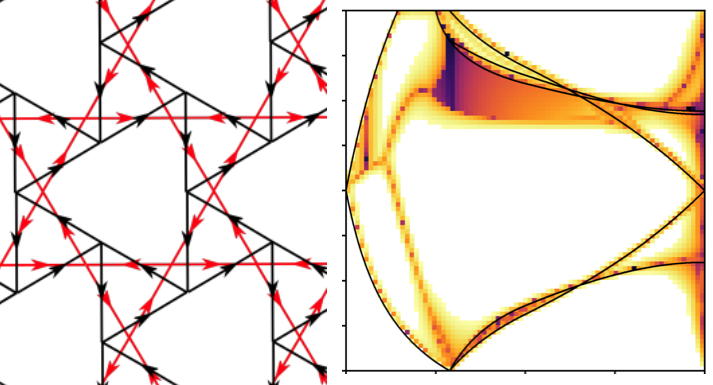
Heat escapes fast due to bulk-edge correspondence
Analyzing a diffusion equation of alternative metals, rapid heat conduction to the heat bath due to edge states is predicted. The edge states are predicted by the bulk topological invariant as a typic...
Read More
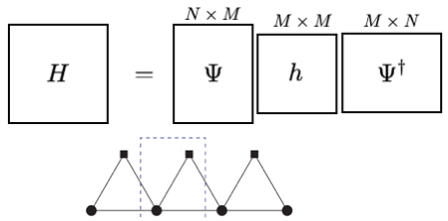
Exact correlation of correlation
Once one admits the electronic state is described by the molecular-orbitals (MOs), the system has flat bands when the number of MOs is less than the total number of atoms. Then it is natural the elect...
Read More
Discriminant and symmetry
As widely accepted, the degeneracy of eigenvalues of the Hamiltonian is a singular point, which is the source of the non-trivial topology. Then it is more than natural that the discriminant of the sec...
Read More
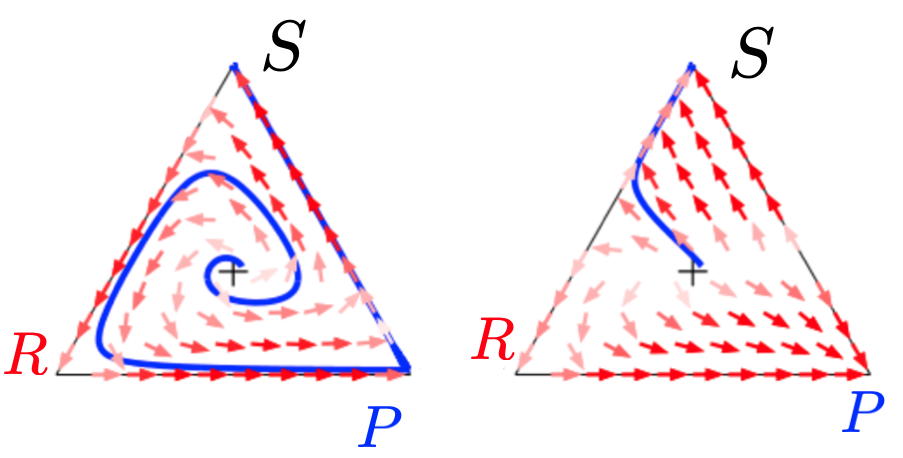
Non-hermitian topology in game theory
The use of topological invariants for the characterization of material phases has been quite successful. Non-trivial topology is reflected by physical observables near the boundaries of systems as a b...
Read More
First/second order topology in honeycomb lattice
The Haldane model with Kekulè distortion possesses various phases characterized by different topology with specific boundary states. Competition between the 1st/2nd order topology (1D/0D boundary stat...
Read More
Flux attachement and bulk-edge correspondence
Adiabatic insertion of the Aharonov-Bohm flux through two pinholes introduces charge transport between them when the system is topologically non-trivial. This is the Laughlin argument. The defects/pin...
Read More
Young Scientist Award of the Physical Society of Japan (2022)
Tsuneya Yoshida (assistant Prof.) is awarded the "Young Scientist Award of the Physical Society of Japan (2022)" Pioneering works on non-Hermitian strongrly correlated phenomena "Non-He...
Read More
BEC Seminar 14:00-15:00 Nov.26 (2021) Yoshiyuki Matsuki
Yoshiyuki Matsuki will be telling us on their recent work. (Zoom)。Join us by contacting Y. Hatsugai. "Fractal defect states in the Hofstadter butterfly"
Read More
Multi-fold EP protected by anti-unitary symmetry
Generic degeneracy of a non-hermitian hamiltonian implies a set of the eigenvectors is not enough to span the total linear space. One needs to extend the idea of the eigenstates to the generic ones, w...
Read More